并查集
若某个家族人员过于庞大,要判断两人是否是亲戚,确实很不容易,根据某个亲戚关系图,现在任意给出两个人,判断其是否具有亲戚关系,规定:x和y是亲戚,y和z是亲戚,那么x和z也是亲戚,如果x和y是亲戚,那么x的亲戚都是y的亲戚,y的亲戚也都是x的亲戚。
算法步骤
- 初始化,吧每个节点所在集合初始化为其自身
- 查找,查找两个元素所在的集合,即找祖宗。注意:查找时,采用递归的方法找其祖宗,祖宗集合号等于本身时停止,在回归时,把当前节点到祖宗路径上的所有节点统一为祖宗的集合号。
- 合并,如果两个元素的集合号不同,将两个元素合并为一个集合。注意:合并时只需要把一个元素的祖宗集合号改为另一个元素的祖宗集合号。“擒贼先擒王”,只改祖宗即可。
假设现在有7人,通过输入亲戚关系图(2-7、4-5、3-7、4-7、3-4、5-7、5-6、2-3、1-5)
初始化,把每个人的集合号初始化为其自身编号。
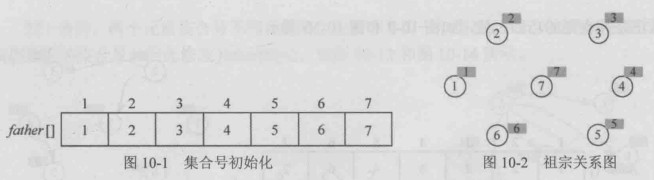 初始化
初始化
输入 2-7
- 查找,查找2所在集合号为2,7所在集合号为7.
- 合并,两个元素集合号不同,将两个元素合并为一个集合,在此约定把小的集合号赋值给大的集合号,因此修改
father[7]=2
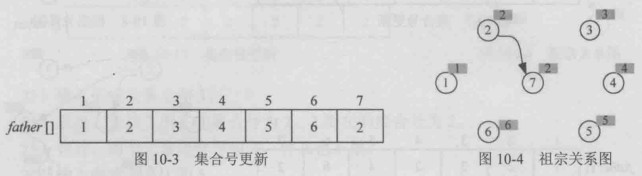 2-7
2-7
输入 4-5
- 查找,查找4所在的集合号为4,5所在的集合号为5
- 合并,两个元素集合号不同,将两个元素合并为一个集合号,将小的赋给大的,father[5]=4
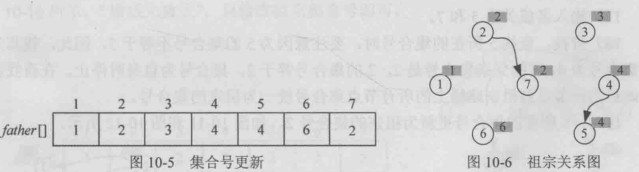 4-5
4-5
3-7
- 查找,查找3所在的集合号为3,7所在的集合号为2
- 合并,两个元素的集合号不同,将两个元素合并为一个集合号,father[3]=2
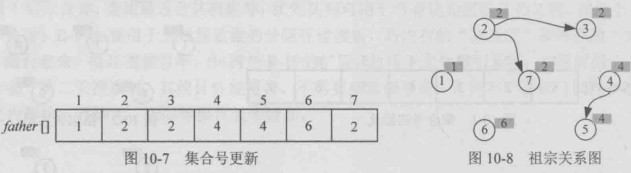 3-7
3-7
4-7
- 查找,查找4的祖宗,4的集合号为4,7所在的集合号为2
- 合并,两个元素集合号不同,将两个元素合并为一个集合,修改father[4]=2,只改祖宗即可,集合号为4的有两个节点,在此只需要修改4的祖宗即可,并不需要把集合号为4的所有节点都检索一遍。
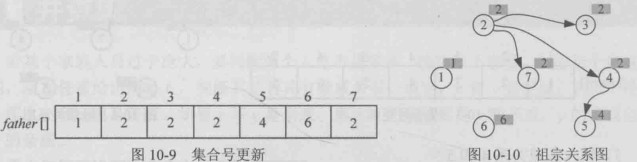 4-7
4-7
3-4
- 查找,查找3所在的集合号为2,4所在集合号为2
- 合并,两个元素集合号相同,什么也不做。
 3-4
3-4
5-7
- 查找,查找5所在的集合号时,要注意因为5的集合号不等于5,因此,找其父亲的集合号为4,4的父亲集合号是2,2的集合号为2,集合号为自身时停止,在查找返回时,把当前节点到祖宗路径上的所有节点集合号统一为祖宗的集合号。father[5]=2
father[4]=2。7所在的集合号为2.
- 合并,两个元素集合号相同,什么也不做。
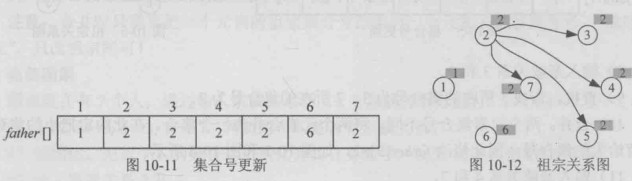 5-7
5-7
5-6
- 查找,查找5所在的集合号为2,6所在的集合号为6
- 合并,father[6]=2
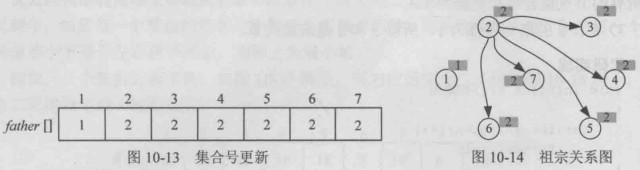 5-6
5-6
2-3
- 查找,查找2所在的集合号为2,3所在的集合号为2
- 合并,两个元素集合号相同,什么也不做。
 2-3
2-3
1-5
- 查找,查找1所在的集合号为1,5所在集合号为2,2所在集合号为2,因此5的祖宗为2
- 两个元素集合号不同,将两个元素并为一个集合,在此约定把小的集合号赋值给大的集合号,因此将5的祖宗2号节点的集合号改为1即可,即修改father[2]=1,只修改祖宗集合号即可。
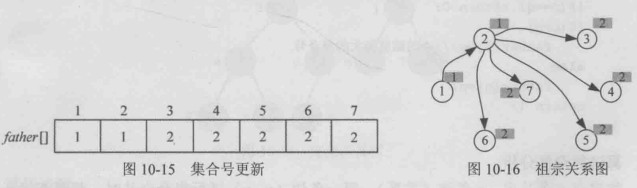 2-3
2-3
到此为止,亲戚关系图已经输入完毕。
可以看到 3、4、5、6、7这些节点集合号并没有改为1,这样可以吗?
- 如果要判断现在有几个家族(集合),只需要统计有几个集合号和下标相同。目前只有1的集合号和下标相同,说明现在只有一个集合。
- 如果要判断两人是否有亲戚关系(是不是属于同一个集合),只需要看这两个人的祖宗是否相同。
代码实现
void Init(int n)
{
for(int i=1;i<=n;i++)
father[i]=i;
}
int Find(int x) //找祖宗
{
if(x!=father[x])
father[x]=Find(father[x]);
return father[x];
}
int Merge(int a, int b) //合并集合
{
int p=Find(a);//找a的祖宗p
int q=Find(b);//找b的祖宗q
if(p==q) return 0;
if(p>q)
father[p]=q;//小的赋值给大的集合号
else
father[q]=p;
return 1;
}
算法复杂度分析
如果有n个节点,e条边关系,每一条边(u,v)进行集合合并时,都要查找u和v的祖宗,查找的路径从当前节点一直到根节点,n个节点组成的树,平均情况下树的高度为logn,因此并查集中,合并集合的时间复杂度为
O(e*logn)。










